Kadane’s Algorithm — (Dynamic Programming)

If you are reading this article then definitely you are getting your hands dirty in data Structure, So first of all more power to you.

I would try my best to make sure you learn the algorithm in the best possible way.

Kadane's Algorithm is very important for students preparing for placements (super important for me), so before starting close your all other tabs!!!

Kadane's Algorithm is used to solve maximum subarray problems (The task of finding the largest possible sum of a contiguous subarray, within a given 1D array)

Wait in an easy way possible, basically, we will be having the input of a one-dimensional array and we have to find the contiguous subarray with the largest sum.

Example:

Input: [-2, 3, -1, 2]
Output: 4
Explanation: Subarray [3, -1, 2] is the max sum contiguous subarray with sum 4.

for solving the problem before going for implementing the algorithm let's go for a simple method.

SIMPLE METHOD:

It involves checking all possible subarrays and calculating their sums to find the maximum subarray sum.

We use two nested loops to iterate through all possible subarrays. The outer loop iterates over the starting index of the subarray, and the inner loop calculates the sum of the subarray starting from that index.

We maintain a "current" variable to calculate the sum of each subarray. We update the "maxSum" whenever we find a larger sum.

Finally, we return the value of "maxSum" which represents the maximum subarray sum in the given array.

USING ALGORITHM :

Kadane's Algorithm is a dynamic programming iterative algorithm. It computes the maximum sum subarray ending at a specific position by using the previous position's maximum sum subarray.

The main principle underlying Kadane's Algorithm is to build the largest subarray sum iteratively by considering each element of the array. The method decides whether to extend the current subarray or start a new subarray from the current element at each step.

Here the whole algorithm revolves around three main keys:

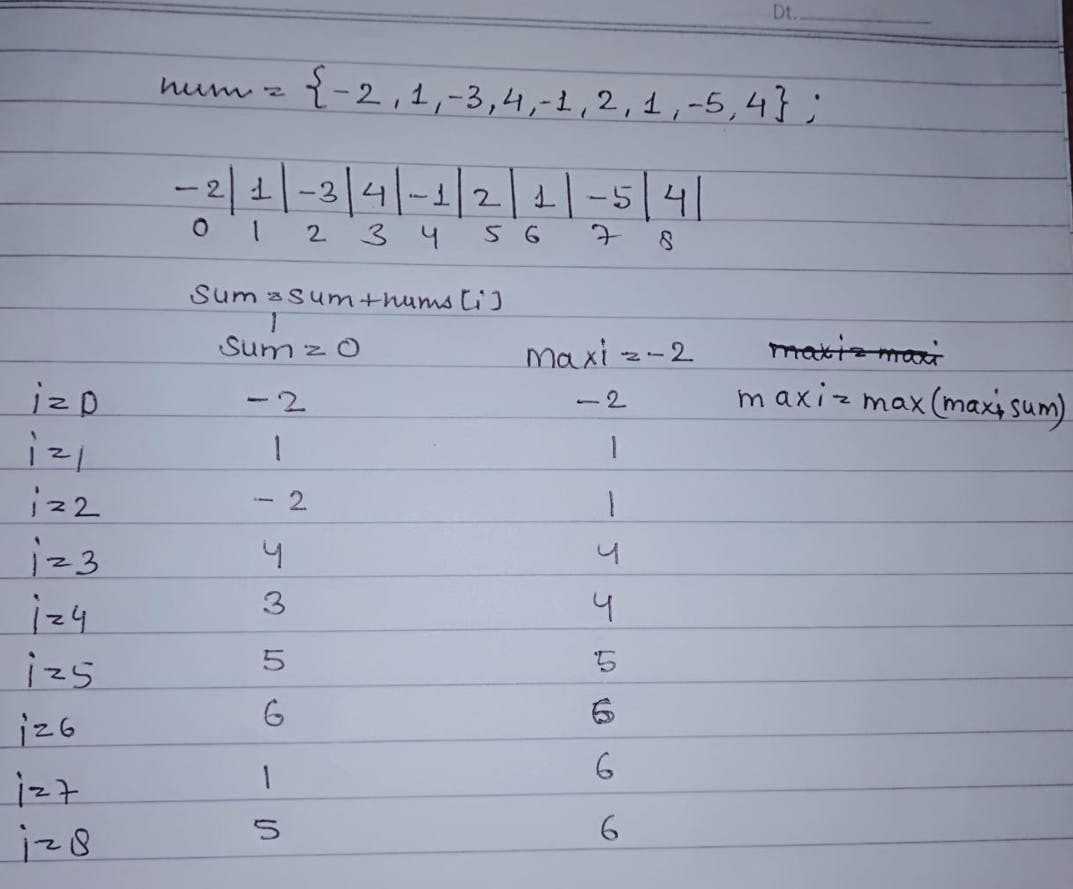
sum = sum + nums[i]

maxi = max(maxi, sum)

if (sum < 0) ,sum = 0

sum is used to track the current sum of the subarray, and maxi stores the maximum subarray sum found so far. Initialize both sum and maxi to the first element of nums (nums[0]).
Update maxi by taking the maximum of the current maxi value and the updated sum value: maxi = max(maxi, sum). This step ensures that maxi always contains the maximum subarray sum encountered so far.
if sum becomes negative. If it does, reset sum to 0. This step effectively handles the case where the sum of the current subarray becomes negative, allowing us to start a new subarray

Dry run:

hope this article was informative to you!!

happy learning:)

just from Student just like you.